javy にビルドを高速化する --no-source-compression オプションを追加した
前回の記事で javy でのビルドが遅い原因について書きました。
あのあとやっぱり気になったので Issue を立てて PR を作成してみました。
レビュワーからのフィードバックもあり当初考えていた圧縮レベルを指定できるオプションではなくソースコードの圧縮をやめるオプション --no-source-compression を追加することになりました。
このオプションを有効にしてビルドすると僕のユースケースでは14秒かかっていたものが3秒になるという結果が得られました。 かなり速くなっていますね。もちろん圧縮をやめるので出力される wasm のサイズは大きくなります。お気をつけください。
1/12 にこの機能を含んだ v1.3.0 がリリースされたのでぜひ試してみてください。
bytecodealliance/javy を軽く調べた

この記事は 0df708ec7b455a4896481a4926eccb23fe6c6014 時点でのソースコードをもとに書いています。詳細は自分で確認してください。
背景
sqlc-gen-typescript が tsc + esbuild + javy を使って作られていてそこで javy の存在を知りました。
TypeScript で wasm のプラグインが簡単にかけるのはすごく便利ですが若干ビルドが遅いと思ったのが調査のきっかけです。
bytecodealliance/javy について
JavaScript を wasm にランタイムごと埋め込んで実行できるようにするツールでランタイムは QuickJS を用いています。
static linking と dynamic linking があって QuickJS を含まない形でも wasm が出力できるようですが今回は static linking のみを調査しました。
(QuickJS を含まない形ってどうやって実行するのだろうか?)
まず swc をライブラリとして使用して JavaScript のパースを行い、export 周りの情報を処理します。
QuickJS を内部で用いている javy_core (wasm として埋め込まれている) に JavaScript を入力として与え、wizer を用いて pre-initialize を行い QuickJS Bytecode 変換まで処理が進んだ wasm を作成します。
作られた wasm を wasm-opt で最適化して、ソースコードセクションに brotli で圧縮した JavaScript を入れて出力します。
なぜビルドが遅いと感じたのか

今回の入力は sqlc のプラグインで JavaScript が 8.5MB でした。
実行には不要なソースコードセクションの JavaScript の brotli での圧縮(最大レベル)に全体の80%である12秒かかっていました。
| 圧縮レベル | wasm のサイズ | 秒数 |
|---|---|---|
| 0 | 80587250 | 0 |
| 5 | 73000152 | 0.5 |
| 8 | 72884233 | 0.8 |
| 11(最大) | 72671954 | 12 |
| ソースコードを含まない | 71659880 | 0 |
圧縮レベルを変更することで速くなることがわかりましたが現時点では圧縮レベルは固定されていて設定で変更できないようになっていました。
圧縮レベルを変更できるようになるか、ソースコードを含まない設定ができるようになればよいなと思いました。
結論
圧縮はオフにできると嬉しいがそういうツールじゃないかも
sqlc internals
sqlc は何をやっているのか、問題に遭遇したときに調査するべき箇所はどこか?
というのを sqlc 1.20 時点の情報をもとに書いていきます。
背景
最近 sqlc に PR を送るようになり sqlc についての理解が深まってきたのでまとめておこうというのと理解を共有しておくことで PR を送る人が増えると良いなという思惑があります。
sqlc とは
SQL Compiler の略でスキーマとクエリからパラメータと結果の型を推論するツールです。 その推論された型からコードを生成したり、lint のようなことが可能です。 コード生成が主な機能ですが v1.20 から sqlc vet が導入されています。
Linting queries — sqlc 1.21.0 documentation
internals
sqlc はスキーマとクエリからパラメータや結果の型を推論しますが流れとしては以下のようになっています。
- parse
- compile
- codegen
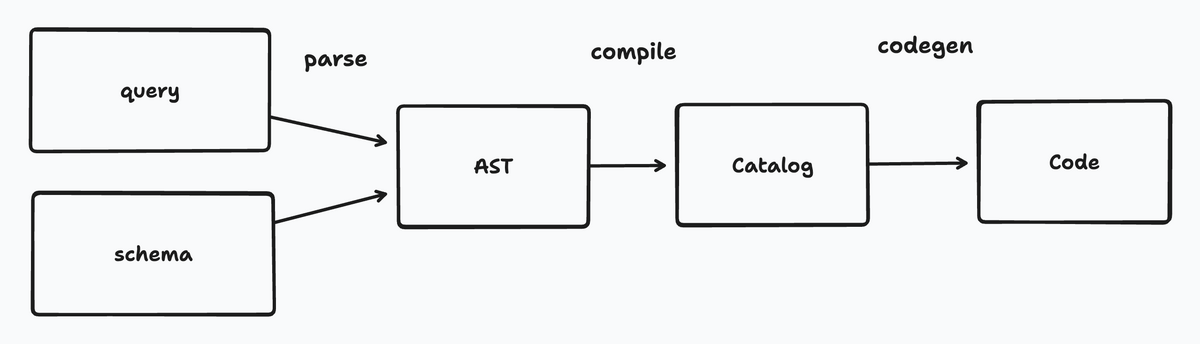
parse
スキーマとクエリをパースします。
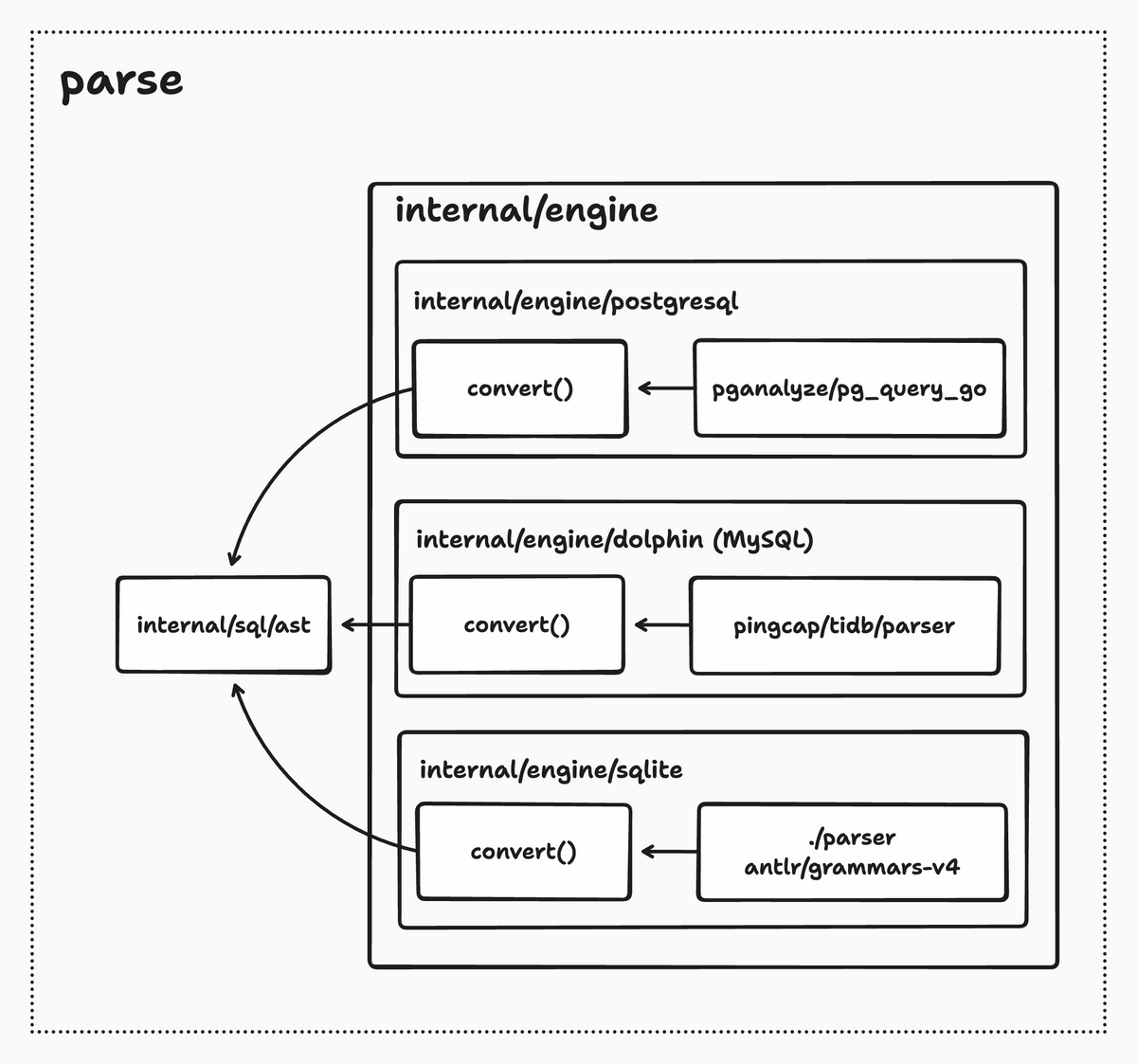
対応しているのは PostgreSQL, MySQL, SQLite の3つで
PostgreSQL は github.com/pganalyze/pg_query_go を使っているので基本的にパースできない SQL はないです。 internal/sql/ast は pg_query_go の ast をベースに作られています。
MySQL は github.com/pingcap/tidb/parser を使っているのでほとんどの SQL はパースできます。 内部のパッケージは internal/engine/dolphin になっています。
SQLite は https://github.com/antlr/grammars-v4 の SQLite の文法をベースに自前のパーサーで処理しています。
sqlc.arg などをパースできるようにするために独自の拡張(SQLite は schema に紐づく関数がないため)が含まれています。
元の文法のルールはエラーにはならないものの正しいノードに分類されていないケースがありそれらの対応も含まれています。
SQLite そのものが持つ柔軟性を再現することが難しいケースがあるため動かない SQL も多々あります。
それそれのパーサーから得られた AST から internal/sql/ast に変換する処理が convert 関数です。 ですが convert 関数の完成度が engine ごとに大きく異なっていて推論が動く範囲で適当な AST を返すようになっていたり そもそも実装時間の都合で未対応になっているものが ast.TODO というノードになっていたりします。
完成度は PostgreSQL, MySQL, SQLite の順になっています。
問題を修正したいときにクエリに対して正しい AST がなにかというのがわからないことが多いです。 基本的に pg_query_go の結果を正として MySQL, SQLite に移植することになります。 pg_query_go は pg_query_go でどのときにどういうノードが返るかについてのドキュメントがないので大変です。
compile
得られた AST から catalog (スキーマの型とクエリのパラメータと結果の型) を生成する処理をコンパイルとしています。
型の推論を AST から行うのですが複雑なクエリだと動かないケースがあります。
interface{} になったりコード生成に失敗したりするケースは明示的に CAST を書くというのがワークアラウンドです。
* の展開や sqlc.embed, sqlc.arg, sqlc.slice などの処理もしています。
特定のカラムやテーブルが見つからないというエラーに遭遇した場合はここで発生しています。 エラーは compile で発生しますが原因が不完全な AST というケースもあります。

codegen
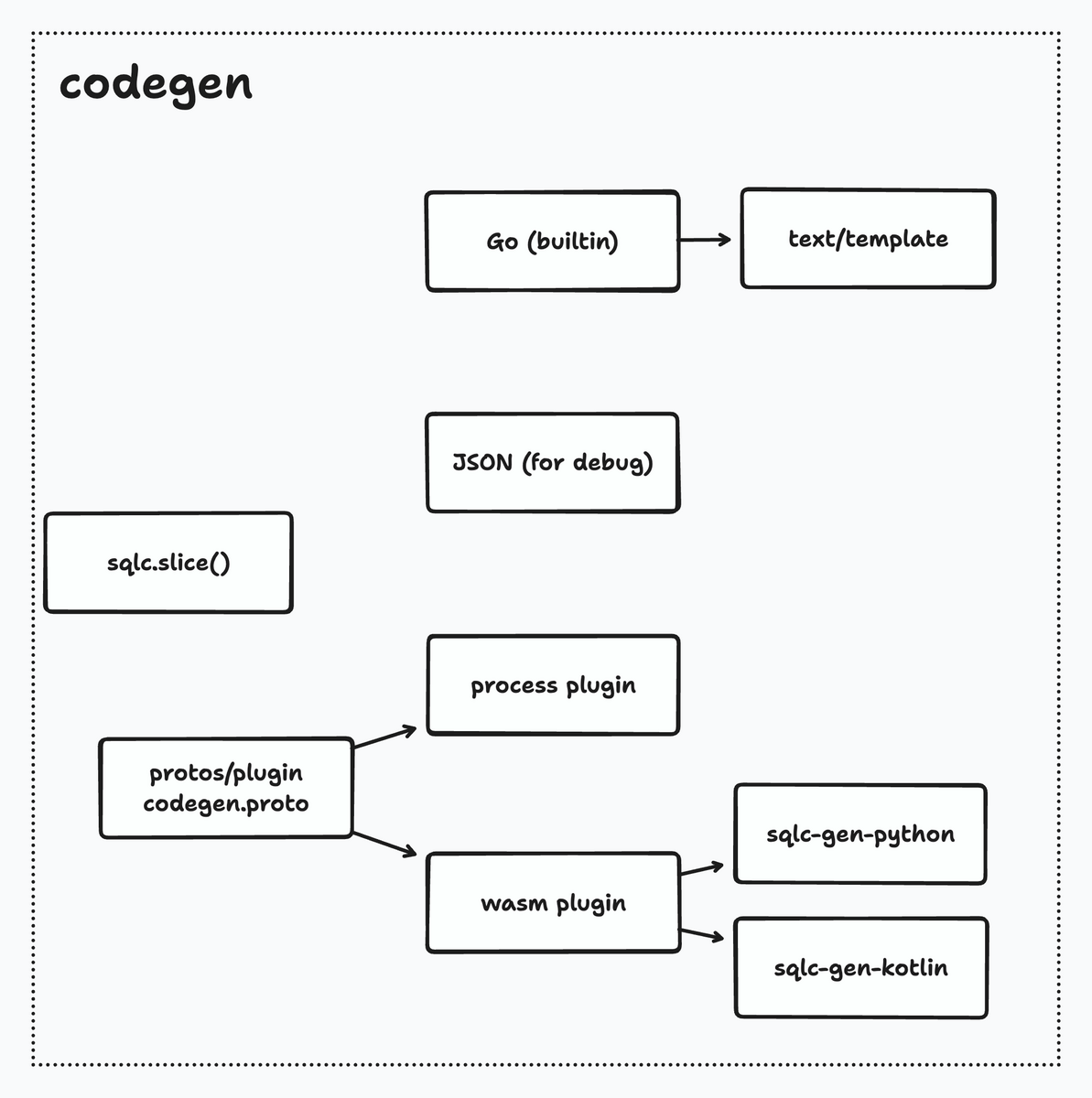
catalog からコードを生成する処理が codegen です。 builtin で go のコードジェネレーターがあります。text/template パッケージが使われています。
sqlc.slice はここでも処理が必要です。
生成コード自体がおかしい場合はここに問題があるケースが多いです。 オプションが多くなってきているので適切にハンドリングできていなかったりします。 もちろん catalog がおかしいケースもあります。
元々は python, kotlin も builtin でしたが切り離されて sqlc-gen-python, sqlc-gen-kotlin になりました。 おそらく debug 用ですが catalog を json を出力する機能もあります。 process plugin と wasm plugin があって wasm plugin が推奨されていますができることが違うので考えて選択する必要があります。
plugin については 前の記事 を参照してください。
builtin の go のコードジェネレーターは簡単に使えますが拡張性はあまりないのでコードが好みではない場合は自分で plugin を書くのが良いと思います。 builtin なのでバグの修正リリースが本体と同じタイミングというところも良し悪しがあります。
debug tips
バグに遭遇したら https://play.sqlc.dev/ で再現するか確認してください。 再現できて自分で修正するのが難しかったりよくわからない場合は issue にしてください。 自分で修正したいと思ったら手元で実行できるようにしてください。
適当に以下のようなツールを作って playground の URL を渡すと go のテストを生成して GoLand でデバッグできるようにしています。
僕がこういう playground に依存したワークフローをしている都合上、issue に playground のリンクがないものの対応優先度がとても低いです。
問題が修正できたら internal/endtoend のテストを編集したり追加したりしてください。 sqlc はほとんどE2Eテストによって動作を確認しています。 ただ internal/endtoend の問題点として一覧性が悪いというのがあります。 修正に対して変更するべきテストがわからないケースは気合で解決する必要があります。
テストの変更・追加が終わったら scripts/regenerate を実行して期待値を更新します。
最後に PR を作れば終わりです。
終わりに
sqlc の内部についてとバグに遭遇したときの対応、どの辺にバグがあるかの勘所を紹介しました。 これをきっかけに sqlc に貢献してくれる人が増えると良いなと思います。
sqlc plugin を書こう
背景
https://github.com/orisano/sqlc-gen-ts-d1 というプラグインを作成していて生成コードの好みが人によって大きく異なると感じることがありました。
一つのプラグインで生成コードをカスタマイズできるアプローチには保守性的な意味でも限界があるだろうと思いました。
気軽にプラグインが作れるようになることで自分の好みのコードが生成できるし、好みが似通ったコミュニティにメンテンスされているプラグインが一つでもあれば幸せな人も増えるかなと思ったため記事を書くことにしました。
とはいえ sqlc を使い始めるとき最初にプラグインを書くことはまずないし、デフォルトの生成コードが好みでなかったりそもそも対応してない場合は選択肢から外れるだけだと思います。
なので sqlc を使いたいという情熱のある人やプラグインを作りたいという人の役に立てばと幸いです。
plugin とは
plugin とは sqlc がパースしたスキーマと結果やパラメータの型が推論されたクエリの情報を使って処理を行うプログラムのことを指します。
大体の場合以下のようなことを行う必要があります。
プラグインを作り始めた段階だと自分に必要な型以外は無視するくらいでちょうど良いです。 コードの生成の際に API の決定をしないといけないのでそこが面倒くさいかなという感じです。
プラグインの提供方式
プラグインの提供方式には以下の3つがあります。
codegen_request.json を使う方式
まず2つのファイルを用意します。
sqlc.json
{ "version": "2", "sql": [{ "schema": "query.sql", "queries": "query.sql", "engine": "sqlite", "gen": { "json": {"out": "."} } }] }
query.sql
CREATE TABLE account ( id INTEGER PRIMARY KEY AUTOINCREMENT, name TEXT UNIQUE NOT NULL ); -- name: GetAccount :one SELECT * FROM account WHERE id = @account_id;
$ sqlc generate
を実行すると codegen_request.json というファイルが生成されます。
{ "settings": { "version": "2", "engine": "sqlite", "schema": [ "query.sql" ], "queries": [ "query.sql" ], "rename": {}, "overrides": [], "codegen": { "out": "", "plugin": "", "options": "" }, "go": { "emit_interface": false, "emit_json_tags": false, "emit_db_tags": false, "emit_prepared_queries": false, "emit_exact_table_names": false, "emit_empty_slices": false, "emit_exported_queries": false, "emit_result_struct_pointers": false, "emit_params_struct_pointers": false, "emit_methods_with_db_argument": false, "json_tags_case_style": "", "package": "", "out": "", "sql_package": "", "sql_driver": "", "output_db_file_name": "", "output_models_file_name": "", "output_querier_file_name": "", "output_files_suffix": "", "emit_enum_valid_method": false, "emit_all_enum_values": false, "inflection_exclude_table_names": [], "emit_pointers_for_null_types": false, "query_parameter_limit": 1, "output_batch_file_name": "", "json_tags_id_uppercase": false, "omit_unused_structs": false }, "json": { "out": ".", "indent": "", "filename": "" } }, "catalog": { "comment": "", "default_schema": "main", "name": "", "schemas": [ { "comment": "", "name": "main", "tables": [ { "rel": { "catalog": "", "schema": "", "name": "account" }, "columns": [ { "name": "id", "not_null": true, "is_array": false, "comment": "", "length": -1, "is_named_param": false, "is_func_call": false, "scope": "", "table": { "catalog": "", "schema": "", "name": "account" }, "table_alias": "", "type": { "catalog": "", "schema": "", "name": "INTEGER" }, "is_sqlc_slice": false, "embed_table": null, "original_name": "", "unsigned": false, "array_dims": 0 }, { "name": "name", "not_null": true, "is_array": false, "comment": "", "length": -1, "is_named_param": false, "is_func_call": false, "scope": "", "table": { "catalog": "", "schema": "", "name": "account" }, "table_alias": "", "type": { "catalog": "", "schema": "", "name": "TEXT" }, "is_sqlc_slice": false, "embed_table": null, "original_name": "", "unsigned": false, "array_dims": 0 } ], "comment": "" } ], "enums": [], "composite_types": [] } ] }, "queries": [ { "text": "SELECT id, name FROM account WHERE id = ?1", "name": "GetAccount", "cmd": ":one", "columns": [ { "name": "id", "not_null": true, "is_array": false, "comment": "", "length": -1, "is_named_param": false, "is_func_call": false, "scope": "", "table": { "catalog": "", "schema": "", "name": "account" }, "table_alias": "", "type": { "catalog": "", "schema": "", "name": "INTEGER" }, "is_sqlc_slice": false, "embed_table": null, "original_name": "id", "unsigned": false, "array_dims": 0 }, { "name": "name", "not_null": true, "is_array": false, "comment": "", "length": -1, "is_named_param": false, "is_func_call": false, "scope": "", "table": { "catalog": "", "schema": "", "name": "account" }, "table_alias": "", "type": { "catalog": "", "schema": "", "name": "TEXT" }, "is_sqlc_slice": false, "embed_table": null, "original_name": "name", "unsigned": false, "array_dims": 0 } ], "params": [ { "number": 1, "column": { "name": "account_id", "not_null": true, "is_array": false, "comment": "", "length": -1, "is_named_param": true, "is_func_call": false, "scope": "", "table": { "catalog": "", "schema": "", "name": "account" }, "table_alias": "", "type": { "catalog": "", "schema": "", "name": "INTEGER" }, "is_sqlc_slice": false, "embed_table": null, "original_name": "id", "unsigned": false, "array_dims": 0 } } ], "comments": [], "filename": "query.sql", "insert_into_table": null } ], "sqlc_version": "v1.20.0", "plugin_options": "" }
catalog にテーブルの情報, queries にクエリの情報がある json です。
この json を用いて適当なコードを出力するプログラムを書いてみましょう。
今回は https://zenn.dev/voluntas/scraps/f8a2de562bac37 の TypeScript の型を生成してみます。
import json def to_camel(x): xs = x.split("_") return xs[0] + "".join(map(str.title, xs[1:])) with open("codegen_request.json") as f: codegen = json.load(f) to_ts_type = { "INTEGER": "number", "TEXT": "string", } for query in codegen["queries"]: name = query["name"] print(f"type {name}Param = {{") for param in query["params"]: param_name = param["column"]["name"] param_type = param["column"]["type"]["name"] prop_name = to_camel(param_name) prop_type = to_ts_type[param_type] print(f" {prop_name}: {prop_type}") print(f"}}") print(f"") print(f"type {name}Row = {{") for column in query["columns"]: col_name = column["name"] col_type = column["type"]["name"] prop_name = to_camel(col_name) prop_type = to_ts_type[col_type] print(f" {prop_name}: {prop_type}") print(f"}}") print(f"")
上の Python スクリプトを実行すると以下の TypeScript が生成されます。
type GetAccountParam = { accountId: number } type GetAccountRow = { id: number name: string }
最も簡単なプラグインの書き方は codegen_request.json を用いたこの方法だと思います。
- 正確にはプラグインではないが同等のことができる
- 基本的にどの言語でもかけるので始めやすい
- プロジェクト専用のプラグインならこれで十分
- sqlc generate で完結しない。シェルスクリプトや Makefile が必要になる
- プログラムの実行環境が必要なので配布が面倒くさい
process plugin として提供する方式
codegen_request.json の方式で生成されていた codegen_request.json と同等の情報が protobuf として渡されます。
https://github.com/sqlc-dev/sqlc/blob/main/protos/plugin/codegen.proto
それを処理するプロセスを提供する方式です。
- protobuf が問題なく処理できて複数のプロジェクトで使いたい場合はこちら
- wasm と違って自由に処理が行える
- 複数のOSに対応する必要がある場合はクロスビルドができないと面倒くさいかもしれない
- クロスビルドができても配布が複数必要になるのが面倒くさい
wasm plugin として提供する方式
protobuf を処理する wasm を提供する方式です。URL と SHA256 を指定します。
https://github.com/orisano/sqlc-gen-ts-d1 が参考になるかと思います。
- 広く使ってもらいたい場合はこちら
- wasm にできれば複数OSを意識しなくてもよい
- 使う側としては process plugin より安全
- ただ手元での開発がめんどくさいことが多い
- file スキームを使うようにする
- sha256 による検証が必須
終わりに
plugin 開発を始めるときは codegen_request.json を使う方式が良いかなと個人的には思います。デバッグのためにも json として出力しておくのがおすすめです。
wasm にできるなら wasm plugin, そうでないなら process plugin というのが良いのではないでしょうか。
ぜひ sqlc plugin を作ってみてください。
次なる pkg/errors を探してを読んで
https://tech.kanmu.co.jp/entry/2023/06/19/150000 を読んで思ったこと、調べたことを書きます。
pkg/errors の移行先を探すという話で
の2つが候補から最終的には cockroachdb/errors を選んでいました。
検討の中で求めるものの1つとして 性能が大きく劣化しないこと があげられていてベンチマークが行われていました。
ベンチマークのソースコードと結果は以下になります。
結果 cockroachdb/errors は goark/errs と比較してパフォーマンスは悪いというものでした。
ここで気になるのが何故パフォーマンスが悪いのかというところです。 ベンチマークを公開する上で数値のみだけではなく何故その結果になったのかという分析も付加されていたほうが良いと言うのが僕の考えです。
追試・検証
実際に上記のベンチマークを手元の環境で実行したところ傾向としては同じでした。
cockroachdb/errors
まずは cockroachdb/errors の flamegraph を見てみます。

cockroachdb/errors では StackTrace の Format が重い事がわかります。 そもそも StackTrace は pkg/errors のものを使用しています。
https://github.com/pkg/errors/blob/5dd12d0cfe7f152f80558d591504ce685299311e/stack.go#L64
Frame.Format はあまり最適化されておらず %+v を使うと Frame ごとに3回 FuncForPC, 2回 FileLine が呼び出されてしまいます。
StackTrace の Format 以外にも strings.ReplaceAll も気になります。 cockroachdb/errors は個人情報を出力しないようにする仕組みが存在しておりその処理で strings.ReplaceAll が使われています。
個人情報を出力しない仕組みの詳細については
を確認してください。
goark/errs
次は goark/errs の flamegraph を見てみます。

まず cockroachdb/errors の方にあった FuncForPC などの関数がありません。 ソースコードを確認したところ出力時に解決するのではなく New したタイミングで解決するようになっています。 しかも New を呼び出した関数名のみを取得します。なので goark/errs は適切にエラーを Wrap しなければスタックトレースになりません。
出力の処理は json.Marshal と fmt.Sprintf を使っています。 json.Marshal を高速化するために goccy/go-json に変えるのもありかもしれません。
まとめ
cockroachdb/errors と goark/errs のパフォーマンス差異の理由は以下
Go 1.15 から io.CopyBuffer はコピー先が *os.File だと指定したバッファーを使わない
TL;DR
Go 1.15 から io.CopyBuffer はコピー先が *os.File だと指定したバッファーを使わない
6/3 21:57 追記
調べてみたら Go 1.15 の Release Note https://t.co/VUcSeYYrZB の os の項目に説明がありました。issue もあるみたいですね https://t.co/q1mhweAV7d
— matsuyoshi (@matsuyoshi30) 2023年6月3日
既知の問題でリリースノートにも書いてありました、情報提供ありがとうございます!
Go 1.15 Release Notes - The Go Programming Language
本題
Go で io.Reader から io.Writer に対してデータをコピーしたいとき io.Copy を使うと思います。
io.Copy は io.WriterTo や io.ReaderFrom が実装されている対象に対してはそれを使います。 そうでない場合は 32 キロバイトのバッファーを使ってコピーを行います。
この 32 キロバイトのバッファーが毎回メモリ確保されるのでループなどで io.Copy を使う場合は予めバッファーを確保しておいて io.CopyBuffer を使うかなと思います。
ですが Go 1.15 からコピー先が *os.File だと io.CopyBuffer が渡したバッファーを使ってくれません。
*os.File は io.ReaderFrom が実装されているのでその分岐に入ります。
*os.File の ReadFrom の実装は以下です。
プラットフォームごとに異なる実装の readFrom に処理が移譲されています。現時点だと実装されているのは linux だけでそれ以外は stub の実装です。
linux の実装も基本的には readFrom の先が *os.File だったときに copy_file_range(2) を使うためのものです。
コピー元が *os.File じゃなければ genericReadFrom にフォールバックして io.Copy が使われてしまいます。(無限ループにならないために Write しか実装してない onlyWriter という型で包んでいる)
ReadFrom にはバッファーを受け取る口がないので渡したバッファーを考慮できません。
結論
io.CopyBuffer はコピー先が *os.File だと指定したバッファーを使いません。
バッファーを指定したい場合は Write のみを実装した onlyWriter で包んで io.CopyBuffer にわたす必要があります。
Apple Silicon だと go tool pprof の Disassemble が動かない問題とその対応
まとめ
macOS ARM64 では -no_pie オプションが使えなくなっていて、現状だと go tool pprof で Source / Disassemble が使えない。
プロファイリング対象のバイナリ自身でプロファイルを書き換えるライブラリを作成し Source / Disassemble ができるようになった。
現状では macOS ARM64 のみ対応している。
背景
go-json の性能改善をしていて benchmark の cpuprofile を pprof で見ようとしたところ Source の機能が使えないことがわかった。
原因調査
バージョン起因の問題であるか確認するために go 1.17, 1.18, 1.19 でも試したが同じ結果だった。
次に環境の問題であるか確認するために linux で試したところ問題は発生しなかった。そのため環境に依存する問題であることがわかった。
なぜ正常に動作しないのかを理解するために cmd/pprof をデバッガを使いながら確認したところシンボルは存在しているがアドレスが異なることがわかった。
また実行するたびにアドレスが変わることもわかった。
ASLR と PIE の具体的な違いを理解していないので ASLR の問題かと思ったが直近有効になったものではなかった。
ASLR について調査していたときに以下の issue を見つけ PIE について思い出した。
PIE について調査すると macOS ARM64 では no_pie が使えなくなっていることがわかった。
cmd/link: pass darwin/amd64-specific flags only on AMD64 · golang/go@612b119 · GitHub
つまり no_pie が使えないため PIE が有効になっていて pprof の Source / Disassemble が動かないということがわかった。
対応
runtime/pprof は SIGPROF を受け取るたびに goroutine の pc を取得し link register をたどって unwind している。
sample としてコールスタックの pc をそのまま書き込んでしまう。
その処理を修正するのは難しいので書き込まれたプロファイルを書き換える方針で考えた。
書き換えるためには実行時の text segment のアドレスが必要なためプロファイリング対象のバイナリ自身でプロファイルを書き換えなければならない。
go:linkname を使って非公開の関数を呼び出して text segment のアドレスを取得し、バイナリに含まれている runtime.text を用いて pc を変換する。
これを行うライブラリを作成し公開した。
非公開の関数を使っているため、将来的には動かなくなる可能性がある。また runtime.text の値が固定であるように見えたのでハードコードしている。
より良い方法があれば教えてもらいたいし、PR を作ってもらえるとより嬉しい。
個人的なユースケースだと go test -bench -cpuprofile でプロファイリングすることが多いのでユーティリティ関数を提供している。
例
package nopieprofile_test import ( "log" "os" "testing" "github.com/orisano/nopieprofile" ) func TestMain(m *testing.M) { code := m.Run() if err := nopieprofile.RewriteTestProfile(); err != nil { log.Printf("warn: failed to rewrite test profile: %v", err) } os.Exit(code) }
上記のようにすると -cpuprofile の先が書き換えられるようになる。
pprof の Source / Disassemble は非常に便利なので使えるようになって嬉しい。